Waveguide Math

And now for a totally non-relationship oriented post (let's see how many comments I get). Taking the curl of Faraday's Law says: Applying Ampere’s Law and a vector identity give: Assuming no sources and losses inside the waveguide requires that: So: None of this is new; we worked out all this math for plane waves. But for plane waves, we said that for a wave propagating in the z-direction, there was no x and y dependence. In other words, E = Ae^-γz, where A was a complex constant. Now we are instead going to assume that E does have an x and y dependence: E = X(x)Y(y)e^-γz, where X(x) and Y(y) are functions of x and y. It follows that the derivatives with respect to x and y contained in the vector Laplacian have non-zero values: Consider only the vectors in the z direction. Rearranging terms gives: Likewise: Now, given the form of our expected solution, E_z = X(x)Y(y)e^-γz, it follows that Dividing through by X(x)Y(y) e^-γz gives: Note that –(γ² + ω²με) must be a constant. Because X”/X and Y”/Y are each only dependent on x and y, respectively, it follows that both X”/X and Y”/Y must also be constants. Therefore let’s assign the constants –M² = X”/X and –N² = Y”/Y so that: M²– N² = –(γ² + ω²με) and γ = √(M² + N² – ω²με). Note: this is the first equation we have developed for γ in this context. You may recall from plane waves that, for a dielectric, γ = jβ = jω√(με). But now have some additional factors to consider. Note that a propagating wave requires that γ have an imaginary component; if γ is real, we simply have an attenuating field. It follows that M² + N² < ω²με. Now let’s assume that X(x) takes the form Ae^λx. It follows that X” = λ²Ae^λx = –M² Ae^λx. So λ = ±jM and X(x) = Ae^jMx+ Be^-jMx = X₁sin(Mx) + X₂cos(Mx), where X­₁ and X₂ are complex. Likewise, Y(y) = Y₁sin(Ny) + Y₂cos(Ny). Therefore: Similarly, for different functions X(x) and Y(y). We could give them subscripts, but we never use them at the same time, so why bother. Armed with these new equations, let’s return to Faraday’s Law and expand the curl of E as described on the back cover of the text: Remembering our z dependency, and separating the vector components, we can write: Likewise, from Ampere’s Law Substituting equation (5) into equation (1) yields: Similarly: Point: If we know the E_z and H_z components, we can find the transverse components! Question: Is there such a thing as a TEM mode (i.e. E_z = H_z = 0) in a waveguide?

Answer: Let H_z = 0; i.e. Gauss’ Law requires that i.e. there are no magnetic sources. Law requires that 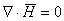It follows that if the transverse components of H are non-zero, the z component of E must also be non-zero!

Likewise, by Faraday’s Law, if E_z = 0 and the transverse components of E are non-zero, then H_z ≠ 0.

Therefore, a waveguide cannot support TEM mode.

Boundary Conditions

Remember that Faraday’s Law requires that the E fields tangent to a surface boundary be equal on both sizes of the boundary, i.e. E_{z, hollow part} = E_{z, metal part}. But inside the metal, σ → ∞, so σE = J = a finite value requires E_{z, inside metal} = 0. Therefore E_{z, hollow part} = 0 at the inside surface of the waveguide. Furthermore, for a wave guide of cross-sectional dimensions a and b, E_x = 0 when y = {0, b} and E_y = 0 when x = {0, a}.

TM Mode: H_z = 0 everywhere inside the waveguide.

Let’s use our equation for E_z we developed earlier: For the boundary x = 0, For the boundary y = 0, So: For the boundary x = a: For the boundary y = b: Plugging in these values for N and M into the equation we developed for Remember that in order to propagate , so the effective cutoff frequency occurs when where v_p = propagation velocity in the dielectric. Note that, because E_z uses the sine function, and sin(0) = 0, both m and n must be greater than zero; otherwise, E_z = 0 and we have no fields for the reason explained earlier.

TE Mode: E_z = 0 everywhere inside the waveguide.

Note: without knowing the surface currents, we cannot directly make any conclusions about H_x and H_y at the boundary. However, we can use the equations we developed earlier, and to say that at boundaries x = {0, a}, At the boundaries y = {0, b}: Given the format of: we can say that: At x = 0, At y = 0, So: At x = a, At y = b, So Notice: because H_z in the TE mode uses the cosine function instead of the sine function, and cos(0) = 1, we can get a wave if either m or n is equal to zero, but not if both are equal to zero. This means that our formula for the cutoff frequency yields as the lowest possible propagation frequency for both the TM and TE cases when a is the larger of the two dimensions, m = 1 and n = 0. We therefore refer to TE₁₀ as the dominant mode.

Spungen writes: "Nice try. There you go with another attempt to reduce propagation, magnetism and dominance to an equation."