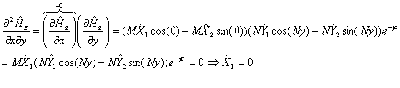And now for a totally non-relationship oriented post (let's see how many comments I get).
Taking the curl of Faraday's Law says:
Applying Ampere’s Law and a vector identity give:
Assuming no sources and losses inside the waveguide requires that:
So: 
None of this is new; we worked out all this math for plane waves. But for plane waves, we said that for a wave propagating in the z-direction, there was no x and y dependence. In other words, E = Ae-γz, where A was a complex constant. Now we are instead going to assume that E does have an x and y dependence: E = X(x)Y(y)e-γz, where X(x) and Y(y) are functions of x and y.
It follows that the derivatives with respect to x and y contained in the vector Laplacian have non-zero values:
Consider only the vectors in the z direction. Rearranging terms gives:
Likewise:
Now, given the form of our expected solution, Ez = X(x)Y(y)e-γz, it follows that
Dividing through by X(x)Y(y) e-γz gives:
Note that –(γ2 + ω2με)
must be a constant. Because
X”/X and Y”/Y are each only dependent on x and y,
respectively, it follows that both X”/X and Y”/Y must also be constants.
Therefore let’s assign the constants –M2 = X”/X and –N2
= Y”/Y so that:
M2–
N2 = –(γ2 + ω2με)
and γ = √(M2 + N2 – ω2με).
Note: this is the first equation we have
developed for γ in this context.
You may recall from plane waves that, for a dielectric, γ = jβ = jω√(με). But now have some additional factors to
consider.
Note
that a propagating wave requires that γ have an imaginary component; if
γ is real, we simply have an attenuating field. It follows that
M2 + N2 < ω2με.
Now
let’s assume that X(x) takes the form Aeλx. It follows that
X” = λ2Aeλx =
–M2 Aeλx.
So
λ = ±jM and X(x) = AejMx+
Be-jMx = X1sin(Mx) + X2cos(Mx), where
X1 and X2 are complex. Likewise, Y(y) = Y1sin(Ny) + Y2cos(Ny). Therefore:
Similarly,
for different functions X(x) and
Y(y). We could give them
subscripts, but we never use them at the same time, so why bother.
Armed with these new equations, let’s return to Faraday’s Law and expand
the curl of E as described on the back cover of the text:
Remembering
our z dependency, and separating
the vector components, we can write:
Likewise,
from Ampere’s Law
Substituting
equation (5) into equation (1) yields:
Similarly:
Point: If we know the Ez
and Hz components, we can find the transverse components!
Question: Is there such a thing as a TEM mode
(i.e. Ez = Hz = 0) in a
waveguide?
Answer: Let Hz = 0; i.e.
Gauss’ Law requires that 
i.e. there are no magnetic sources.
Law requires that 
It follows that if the transverse components of H are
non-zero, the z component of E must also be non-zero!
Likewise, by Faraday’s Law, if Ez = 0 and the transverse components
of E are non-zero, then Hz ≠ 0.
Therefore,
a waveguide cannot support TEM mode.
Boundary Conditions
Remember
that Faraday’s Law requires that the E fields tangent to a surface
boundary be equal on both sizes of the boundary, i.e. Ez,
hollow part = Ez, metal part. But inside the metal, σ → ∞,
so σE = J = a finite value requires Ez, inside metal = 0. Therefore Ez,
hollow part = 0 at the inside surface of the waveguide. Furthermore, for a wave guide of
cross-sectional dimensions a and b, Ex = 0
when y = {0, b} and Ey = 0 when x = {0, a}.
TM Mode: Hz = 0 everywhere inside the
waveguide.
Let’s use our equation for Ez we developed earlier:
For the boundary x = 0,
For the boundary y = 0,
So: 
For the boundary x = a:
For the boundary y = b:
Plugging in these values for N and M into the equation we developed for 
Remember that in order to propagate 
, so the effective cutoff frequency occurs when 
where vp
= propagation velocity in the dielectric.
Note that, because Ez uses the sine
function, and sin(0) = 0, both m and n must be greater
than zero; otherwise, Ez = 0 and we have
no fields for the reason explained earlier.
TE Mode: Ez
= 0 everywhere inside the waveguide.
Note: without knowing the surface currents, we
cannot directly make any conclusions about Hx
and Hy at the boundary. However, we can use the equations we
developed earlier,
and
to say that at boundaries x = {0, a}, 
At the boundaries y = {0, b}: 
Given the format of: 
we can say that: 
At x = 0,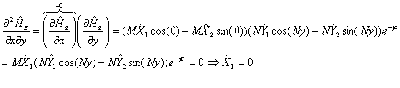 
At y = 0, 
So: 
At x = a, 
At y = b, 
So 
Notice: because Hz in the TE mode
uses the cosine function instead of the sine function, and cos(0) = 1, we can get a
wave if either m or n is equal to zero, but not if both are equal to zero. This means that our formula for the
cutoff frequency yields 
as the lowest possible propagation frequency for both the TM
and TE cases when a is the larger of the two dimensions,
m = 1 and n = 0. We therefore refer
to TE10 as the dominant mode.
Spungen writes: "Nice try. There you go with another attempt to reduce propagation, magnetism and dominance to an equation."
Posts
I wish I had brought my camera to take a color photograph here. Note that the sanctuary has not one, not two, but three video screens at the front. During the service I attended, the round screen in the middle carried kaleidoscopic images of . . . I'm not sure what, but it looked like something from Windows Media Player. The two on the side carried the words to the praise songs set against a background of clouds, trees, oceans and whatnot.
