GRE Percentiles: The Affirmative Action Effect

In my last post, I examined the graduate school exam percentile score data as published by Steve Sailer, and discovered that the low percentage of black college graduates scoring above the white median (~16% for the GRE) is partially but not fully explained as an artifact of the different distributions of ability between blacks and whites: specifically, that the black mean in cognitive ability is one standard deviation below the white mean.

In this post, I will examine whether affirmative action in college admissions affects these results. Based on my initial model, the answer, by inspection, would be: no effect. No student, black or white, magically acquires cognitive ability by the mere fact of college admittance. If +1 SD ability (i.e. an IQ of 115) is necessary to graduate from a competitive college, then admitees with lower ability would simply fail to graduate.

But this analysis ignores the fact that college admissions criteria only estimate a student's ability. There is no bias in these criteria, but there is error: as any college registrar can tell you, some students do, in fact, outperform their admissions portfolio . . . and other students underperform it. I myself saw students with 800 math SAT scores earn C's in calculus. I also saw students with a score of 540 earn the same C.

Thus, students taking the GRE have met two complementary standards: they tested well enough to meet the college admissions criteria, and then they performed well enough to graduate. So, if a college relaxes its admissions standards for black applicants, but maintains the standards for graduation, some of the affirmative action admits will succeed in meeting the higher standard. As has been amply documented, such policies come with great human costs: the greater majority of the AA admits will not graduate, but enter the work force with less work experience, a mountain of debt, and no credential.

Our extended analysis makes use of a two-dimensional probability distribution f as a function of tested ability t (in other words, their composite admissions portfolio as determined by the college) and demonstrated performance p (their actual ability in college). This pdf is defined by the equation:

Let's go over these variables one at a time: μ-bar is a vector of the tested mean μ_t and the performance mean μ_p. σ_t and σ_p are the tested and performance standard deviations. ρ is the correlation coefficient, a measure of how much variation exists between tested ability and demonstrated ability. If ρ = 1, then the admissions tests would absolutely predict performance; this was the unstated assumption in my previous post. If ρ = 0, then the two variables bear no relationship to each other. In practice, ρ will fall between 0 and 1. Σ is called the covariance matrix and is a convenient way of representing the data.

As before, we will model the white population as a standard distribution: μ_t = μ_p = 0 and σ_t = σ_p = 1. (There is no reason to suppose the tested and performance means and variances differ with respect to each other. I will arbitrarily set ρ = 0.5. For those who think this estimate is too low, let me say that from my experience, admissions criteria are not nearly as accurate a predictor as most people think. Using my earlier example, I once ran a regression between math SAT scores and performance on Calc I. The correlation coefficient was about 0.3. I imagine that other factors (GPA, extra curricular activities, etc) improve on that estimate, but I would be surprised if we exceed 0.5. So our 2D pdf is now:

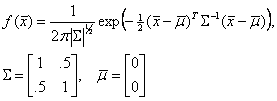
As before, we will expect our GRE-takers to have met a +1 SD standard along both the tested and the performance dimensions. I have started to question this parameter, because the number of students meeting both standards is (by my calculation; your mileage may vary) only 6%, down from 16% for a single standard. This implies that more than 60% of students testing above +1 SD fail to perform at that level. Since graduation rates are higher than that at competitive colleges, then assuming my other parameters are correct, I am guessing that many if not most of their admissions committees build a margin of error into their admissions standards.

Returning to the GRE: assuming that GRE takers have successfully met the +1 SD standard along both dimensions, we can calculate the median performance p_med by:

where t_c = p_c = 1. I computed this as p_med = 1.5, slightly higher than the result for as single dimension.

We will model the distribution of black ability as:

We will then calculate the percentage of black test takers who exceed p_med:

If we assume that black test takers were admitted without affirmative action, i.e. the admissions cuttoff for blacks is the same for whites, t_cb = t_c, then the percentage of blacks meeting the white median climbs to 38%. But let's assume that the college has a quota for blacks, and admits them up from +1 SD from the black mean or up from the white mean of zero. If t_cb = 0, then %_med = 31%.

In conclusion, the affirmative action assumption, applied to our two-dimensional model, brings our calculated value for the black percentile a little closer, but still some distance from the actual percentile of 16%.