In my last lesson, I defined four radiometric quantities:
- Exitance (M): the power density emitted by a surface, measured in Watts / m2. We will reserve B for the per-micron un-integrated quantity.
- Radiance (L): the power density emitted by a surface into each solid angle, measured in Watts / m2 / steradian.
- Intensity (I): the power emitted by a point source into each solid angle, measured in Watts / steradian.
- Irradiance (E): the power incident upon a receiving surface, measured in Watts / m2.
Radiance is the amount of power emitted into each differential solid angle from each differential area perpendicular to that angle. For a lambertian surface, it is by definition a constant:
where Φ is the power in Watts.
In units of steradians, a differential solid angle dΩ measures the ratio between the surface of a sphere subtended by that angle and the square of the sphere’s radius, much in the way an angle in radians measures the ratio of the length of the arc it subtends and the radius of the circle. Note that the subtended surface area of a sphere is only an approximation of the subtended area of a flat surface; however, the approximation is good enough at small angles, and exact at differential angles, which is what we are intending here.
Did you notice the little perpendicular sign after the differential sending area dAs? This is to remind us that the perpendicular area (i.e. the cross-sectional area as it appears from the direction of observation) bears the relationship to the true area shown in the figure below.
This relationship applies to both the receiving area dAR and the sending area dAs, as shown here:
Using these definitions and basic trigonometry gives us the following relationships:
We now have enough equations to solve for exitance M in terms of radiance L by integrating over the surface of a hemisphere defined by the differential surface area dAR:
First, we point out that the hemisphere is always facing the center, hence θR =0°, so cosθR =1. Next, we replace dAR with the area element for integrating over the surface of a sphere in polar coordinates:
dα conveniently integrates out to 2π, and the R2’s cancel. We’re only integrating over a hemisphere, so θs ranges from 0 to π/2. Thus:
This relationship, M = πL for a lambertian surface, is sufficiently rigorous that Planck’s formula itself is often expressed in terms of radiance rather than exitance. However, relating these quantities to irradiance and intensity often make use of assumptions which are less than intuitive. We will examine these assumptions in the next post.








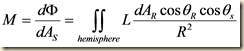

No comments:
Post a Comment