Let’s imagine a differential emitting area dAs on a spherical emitting surface of radius re at a distance R from a differential receiving surface dAR. dAs is at distance R’ and aspect angle γ from dAR; dAR is at aspect angle θ to dAs. Also dAs is at an angle φ from the point of nadir to dAR. In summary,
Applying the Law of Sines gives us:
allowing us to solve for both θ and γ in terms of φ:
The Law of Cosines gives us:
These relationships will be important later.
Radiance is the amount of power emitted into each differential solid angle from each differential area perpendicular to that angle. For a lambertian surface, it is by definition a constant:
In units of steradians, a differential solid angle dΩ measures the ratio between the surface of a sphere subtended by that angle and the square of the sphere’s radius, much in the way an angle in radians measures the ratio of the length of the arc it subtends and the radius of the circle.
We must also bear in mind that the perpendicular area (i.e. the cross-sectional area as it appears from the direction of observation) bears the relationship to the true area shown in the figure below.
Substituting into our equation for radiance gives us:
The quantity in which we are interested is irradiance E, the power per unit area entering our differential receiving area, dAR. Solving for this quantity yields:
The differential surface area of a sphere, dAs, is the standard calculus formula:
where dα integrates around the circle of the visible surface to 2π, and the interior body angle ranges from 0 to the point where γ is a right angle. A simple application of the definition of a cosine yields:
Substituting in these values gives us our final integral:
We will evaluate this integral in our next lesson.





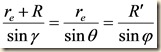




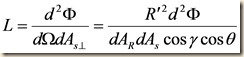



No comments:
Post a Comment