A Derivation of the Variance for the Poisson Probability Distribution

Last week, I searched that Font of All Wisdom, the internet for a derivation of the variance of the Poisson probability distribution. The Poisson probability distribution is a useful model for predicting the probability that a specific number of events that occur, in the long run, at rate λ, will in fact occur during the time period given in λ.

For instance, let’s say that you are waiting at a bus stop for a bus that is known to come at an average rate of λ equals once per hour. But there is no schedule, and you are not guaranteed that the bus will come by exactly once in the next hour. It might come by two or more times, or it might not come by at all. So what is the probability that it comes by k times in the next hour? The probability is given by: 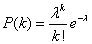where “e” is an irrational number that equals approximately 2.718, and the exclamation point is the factorial function, where k! = k(k-1)(k-2)…(2)(1), all multiplied together. (Note: 0! = 1, for some strange reason.) Wikipedia has an acceptable derivation of this formula, so I will not reproduce it here. Applying this formula to our example, the chance that a bus whose average arrival rate is λ = 1 visit/hour will not come by in the next hour is P[#visits = 0] = 1⁰e^-1/0! = e^-1 = 0.368 = 36.8%. The chance that it will come by exactly once in the next hour would be P[#visits = 1] = 1¹e^-1/1! = 36.8% as well. The chance that the bus will come by exactly twice is P[#visits = 2] = 1²e^-1/2! = 18.3%. These probabilities continue to diminish for increasing numbers of busses predicted to come by in the next hour. As you might expect, the sum of these probabilities = 100%; you are guaranteed that zero or more busses will visit your bus stop in the next hour!

A more useful probability would be, what is the probability that one or more busses will come by in the next hour? Because the probabilities sum to 100%, the math can be done thusly: P[#visits ≥ 1] = 100% - P[#visits = 0] = 100% - 36.8% = 63.2%.

But what if you don’t want to wait an hour? What if you want to catch a bus in the next 15 minutes? This can be easily done by subdividing the rate λ. A bus whose average visit rate is once per hour also has a average visit rate of ¼ visits per 15 minutes. Again to our formula: P[#visits ≥ 1|λ = ¼] = 100% - P[#visits = 0|λ = ¼] = 0.25⁰e^-0.25/0! = e^-0.25 = 100% - 77.9% = 22.1%. Considerably lower probability for a visit in the next 15 minutes.

What if we want to know the average number of busses that will come by in the next hour. Answer: duh! We already told you that the busses come by at rate λ = 1 bus per hour! But let’s derive this from first principles.

To start, we must remember the Taylor Series expansion for e: Because the factorial function is undefined for arguments less than zero, the summation is independent of indices less than zero. Thus: etc.

We also need the definition of the mean, or expected value μ = E(N) of a quantity N whose distribution is defined by P(n). This definition is: μ = E(N) = ∑nP(n) for all n. We can apply this formula to calculate the mean of the Poisson distribution: As expected.

But what about the variance? The variance is a measure of how far a typical result will depart from the average result. In our example, for instance, we know that, on average, we can expect one bus to visit the bus stop each hour. But that number could be zero busses, or it could be multiple busses. So how much variation can we expect? The standard deviation σ is the average that we can expect a particular number of busses to vary from the average number of busses. The variance is the square of the standard deviation, or σ². It is defined thus: σ² = E[(N – μ)² = ∑(n – μ)²P(n) for all n. Applying this formula to the Poisson distribution: So, the variance of a Poisson distribution with average rate λ is . . . λ.

QED.

BLEG: I created the post above on my Dell laptop. I composed the equations in MS Word 2003's MathType, and saved the document as an HTML file. This created the .gif files containing the equations that you see above. But when I tried follow the same process using my desktop computer, When I tried to create the webpage using the exact same methodology, except on my desktop, the equations came out looking like this: Relatively ugly. Clearly, there is some setting that is set correctly on my laptop that is set incorrectly on my desktop, but I don't know what it is. Please help.