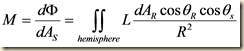It is said that the lottery is a tax on people who are bad at math. What is intended by this is that the odds of winning the lottery as so miniscule that a rational cost-benefit analysis would recommend against participation. But is this always true? Since the jackpot “rolls over” and accumulates for successive drawings, is there some threshold at which the value of a lottery ticket exceeds the price?
Let’s consider the Megamillions lottery played Tuesday night. As has been well documented elsewhere, the probability of buying a winning number for a particular draw can be calculated thus:
Lottery Math
| Number of balls in main cage: | 75 |
| Number of balls drawn from main cage: | 5 |
| Number of balls in Megaball cage: | 15 |
Number of possible combinations of the six balls:
Probability of drawing correct number:
It follows that if the net present value of the lottery jackpot exceeds $N, then a $1 lottery ticket becomes a good investment. Correct?
First, consider that the net present value of the lottery jackpot is not the advertised jackpot. The one-time payout for last week’s $636M jackpot is only $340M, whose value is then diminished by federal, state, and local income taxes at (roughly) 45%. So the winner’s after-tax take is only $187M.
Yet not even this is the net present value. We must also consider the probability that, as happened last night, the jackpot is shared between multiple winners. What is that probability?
Number of Tickets sold: T
The probability that at least one winning lottery ticket (i.e., w ≥ 1) would be sold: p(T)
Each successive ticket t purchased adds to the total probability of a winning ticket p(t) the probability P multiplied by the probability that none of the earlier tickets were successful, which is 1 – p(t-1). Thus:
Last week’s drawing had 336M participants. Thus:
for P as calculated above.
We included in that that 73% probability the chance that multiple winning tickets were selected. But since multiple tickets means splitting the prize, then the expected value of the prize is the jackpot divided by the expected (e.g., the average over multiple trials) number of winners. Can this be calculated?
In general, the formula for the expected value of random variable W is
i.e., the sum, over all possible values of w, of the product of w and the probability of w. In this case, W is the random variable describing the number of winners, w is a specific number of winners, and p(w) is the probability of that w winners.
Given P as calculated above, let’s shift variables and designate p(T,w) as the probability of exactly w winners given T tickets sold.
The probability of one winner when one ticket is sold: p(1,1) = P
The probability of one winner when two tickets are sold:
The probability of one winner when three tickets are sold:
In our application, the number of tickets T is presumably fixed and known. We are also interested in knowing how the probability changes with w, the number of winners. Each ticket is an independent event, so:
The probability of two winners when two tickets are sold: p(2,2) = PP = P2
The probability of two winners when three tickets are sold:
“Wait a second!” the astute among you are saying about now, “that’s starting to look like the binomial theorem!” Indeed it does. In fact, we can generalize that for exactly k winners among T tickets sold, the probability is:
i.e., the product of the probabilities of all winners and losers and the number of ways we can combine them.
In our calculation of the expected value, it would be nice if we could apply the binomial theorem,
but we can’t, because we must weight the terms by as written, because we must weight the terms by w:
Unfortunately, I’m not good enough at math enough to figure out a closed-form solution to the summation above without knowing the answer in advance. And the usual way of evaluating , with factorials as show above, won’t work when T is hundreds of millions of tickets sold; no computer generates factorials that large. But the Wikipedia article suggests using iteration and logarithms to calculate
for large T, which I have done in Matlab here:
%%
% Parameters
n = 75; % Number of balls in main bin
v = 5; % Number of balls drawn from main bin
m = 15; % Number of balls in MegaBin
N = m*nchoosek(n,v); % Number of possible lottery combinations
P = 1/N; % Probability of receiving the winning number
%
% Calculate the binomial coefficients with logarithms
%
T = N; % Arbitrarily set the number of number of tickets sold to 239E6; we vary this number over multiple runs
i = 1:T; % A vector containing all integers between 1 and T
logi = log(i); % Calculate the logarithm of all integers between 1
% and T
logu = 0;
logl = 0;
for k = i,
logu = logu + logi(T-k+1);
logl = logl + logi(k);
logBC(k) = logu – logl; % the natural log of the binomial coefficient, i.e. log[(T k)]
end;
% Calculate the expected value
logP = log(P);
logQ = log(1-P);
% natural log of the product of k wins and the probability of k wins
logwpw = logi + logBC + i*logP + (T-i)*logQ;
EW = sum(exp(logwpw)); % Calculate the antilog and sum
display(EW);
Fortunately, on a Xeon X5672 at 3.2GHz, this algorithm can be executed in a few minutes; note, however, that I optimized it for speed by minimizing the contents of the for loop. The tradeoff is that I have several N-length floating-point vectors that managed to take up 18GB of memory. Proceed at your own risk!
I ran the program for several values of T, and convinced myself that E[W] = T/N = PT. Now that I know the answer, I’d like a second crack at a closed form solution:
I will now resort to a bit of hand-waving: given values of T in the hundreds of millions, the value for E[W] is not measurably diminished by conditioned on a given number of winners. This is analogous to the probability of rolling double-sixes given that you already rolled one six. (Answer: 1/6, not 1/36.) So given that you won the jackpot, the number of additional expected winners is still PT.
Applying this to the problem at hand, it follows that the after-tax value of last night’s jackpot must be divided through by 1 (i.e., you) + 336/259 (the other winners), reducing the value of your jackpot share to $81M.
Now, it is theoretically possible that, given a high enough jackpot, that $81M could increase to the $259M necessary to make the expected value of the lottery ticket greater than the dollar you’re paying for it. But remember that the number of tickets T for any given drawing will probably go up with the increasing jackpot, diminishing its value to an individual player. And even if it didn’t, it wouldn’t follow that buying multiple tickets would be a good idea. I will leave working the math out to the reader, but you would be assured of buying duplicate tickets, and thereby playing against yourself, after a few tens of thousands of tickets purchased, and the model would need to be extended to account for this.
(NOTE: The foregoing was for entertainment purposes only. Those wishing to invest their life savings in lottery tickets should consult a qualified dissipation professional.)




![clip_image002[8] clip_image002[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEge9HSpoKjKwJnGAE97iQBPIyxDnseBUdqTDGih4CJU5Ccy81Kpm3tIg2I94zqr6YsX7ZZVC8bMZ8ohegaWJhYFXpS72RW_oH4-Jo0LWpjiUYkD3Mct-28i5BSAcSesHSpzESWRCg/?imgmax=800)
![clip_image002[14] clip_image002[14]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiLZaVkhRA7Wdsu1WMYspIaOuPMbpbSiU9EPLV-RPmqxraVm7824kLYrwLW5bfUMO7A5W4N8AMX7_zcuxVT5vux213j4bDK4xahyphenhyphenUdsyANk_sR42znrK-q6wNfFX5zsg6a9UGNpAg/?imgmax=800)
![eqn10_thumb[4] eqn10_thumb[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiIjTMIlBmBgRuQ7rEp5x93iQxT0_SDO6-nfDcn8Lwt-wMTLpN1C4HSF6WOq0yRAyyohbQ7JU_6RsNNWTNt9JrPhXdJz2GxWyKMo0bu61upSgVbgr-rQJS9F_RtIGizFKKB0ajxEA/?imgmax=800)






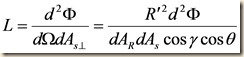



![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgfKOK8tE-RaDN0N0lUUOAEOvD7IpUAWRdjXUc3RXJukPWBPz7f7eWp-jWmETtyZsLVwBymyOwTeiyjyrPcPp5jyDgmNtwoi5gmr5QSnPwVkAYB6kFuWMT-WFPWOgU3QZ__kCNWgg/?imgmax=800)
![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiMPfxU8tlmsnBGJ_SSedphoObAIv_Lbezqdfvr7Bf3G8TLdr4R-sCOUssuWCJow3qAtldD2OrnPnV-CpJ0YTPp1zSy0qYVJaxPjlX1d1vLFD9wpYB74egEFfad0tWiRvV7WvN5Q/?imgmax=800)